Modelo canónico de generaciones solapadas

En macroceonomía, podemos encontrar, por lo general, dos tipos de modelos según la representación de los agentes: los de un agente representativo que vive infinitamente o hasta T (que se puede interpretar como un agente dinástico, que existe cuando hay altruismo entre generaciones y las preferencias son Gorman agregables [habrá futuro post de esto para azote de postkeynesianos]) y la segunda posibilidad es la de generaciones solapadas. En esta última alternativa, hay una función de utilidad que representa una generación y esta vive por un periodo de tiempo finito. Normalmente se asume que no hay altruismo entre generaciones, ya que si adicionalmente se mantuvieran ciertas propiedades de las funciones de utilidad constantes a lo largo del tiempo, estos modelos podrían ser representados como un modelo de un agente ( continuo de agentes entre 0 y 1) que vive infinito tiempo. La ventaja de estos modelos es que nos permiten analizar cuestiones que requieren una composición demográfica más rica, como cuestiones relativas a la seguridad social. Es un modelo muy sencillo, pero tiene aplicaciones muy interesantes, desde el efecto de incrementos del tipo de interés nominal en el precio de burbujas racionales hasta modelos de la crisis de la deuda soberana en la euro-zona (el segundo paper es bastante más asequible que el primero).

Pues bien, en mi clase de Macro estábamos dando el material del capítulo 9 de ‘Introduction to Modern Economic Growth’ de Acemoglu (diapositivas). Como curiosidad el profesor añadió que la variación de ciertos parámetros, como la time preference (beta), entre un valor ‘alto’ (H) y otro ‘bajo’ (L) que cambiasen entre generaciones, para generar fluctuaciones que dependieran de diferentes características (determinadas aleatoriamente) de las generaciones que van entrando en el llamado canonical model (ver las diapositivas linkeadas). En concreto, el time preference (beta) seguía el siguiente proceso:

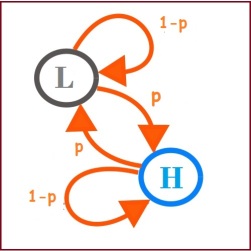
Si nos encontramos que la generación joven de hoy (la que decide cuando ahorrar) tiene una time preference ‘baja’ (L) , con probabilidad p la siguiente generación va a tener una time preference ‘alta’ (H) y con 1-p seguirá siendo ‘baja’ (L), lo mismo cuando partimos desde el caso de H.

Cogemos el caso donde la utilidad es logaritmica y una funcion de producción Cobb-Dougglas con TFP Hicks neutral y L crece a una tasa constante:

Gracias a este ultrasencilla aplicación (aunque también se recomienda probar otras funciones de utilidad y de producción) los efectos de sustitución y renta se anulan y queda una law of motion del capital extremadamente sencilla. El resto de variables como el consumo, la producción y demás son facilmente obtenibles una vez sabemos los valores del capital.

 

 

Vamos a simular el modelo, partiendo de un estado de la time preference arbitrario y un nivel de capital arbitrario, computar la evolución del capital durante 10000 periodos y ver el gráfico y histograma de este previamente eliminando las primeras 100 iteraciones (para eliminar la convergencia desde ese valor arbitrario de capital inicial).

 ## SIMULATION OF THE TIME PREFERNCE FLUCTUATIONS IN AN OLG MODEL

# TIDY UP
rm( list=ls() )

# PACKAGES & LIBRARY
install.packages("markovchain")
library(markovchain)

#CALIBRATION
alpha = 0.75 #capital share of the economy
betaH = 0.95 #time preference of the patient generations
betaL = 0.85 #time preference of the impatient generations
A = 5 #Fixed level of technology, or total factor productivity
n = 0.02 #exogenous rate of population growth
k0 = 1 #initial level of capital, must be > 0 to avoid the destruction (unstable) steady state
p = 0.5 #probability that the next generation has a different time preference from the previous one

#TIME PREFERENCE PROCESS
#Manual for the markovchain package: https://cran.r-project.org/web/packages/markovchain/vignettes/an_introduction_to_markovchain_package.pdf
statesNames=c(betaH,betaL)
betaprocess <-new("markovchain", transitionMatrix=matrix(c(p,1-p,p,1-p),byrow=TRUE,
nrow=2, dimnames=list(statesNames,statesNames)))
plot(betaprocess)
beta <- rmarkovchain(n = 10000, object = betaprocess, t0 = betaH)

#CAPTIAL LAW OF MOTION
k = rep(0,10000)
k[1] <- k0
for (i in 2:10000) {
k[i] = (1/(1+n)) * (as.numeric(beta[i-1])/(1+as.numeric(beta[i-1]))) * (1-alpha) * A * (k[i-1])^alpha
}

# CLEANING AND PLOTTING THE RESULTS
clean_k <-k[100:10000]
hist(clean_k)
plot(clean_k, type='l')

Arroja los siguientes resultados:

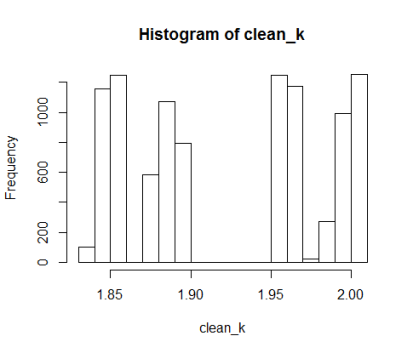
Pfff, que feo. Bien, pues se supone que la distribución de clean_k debería ser casi normal  (con las colas cortadas) cuando p es alrededor de 0.5 y mas como exponenciales (crecientes y/o decrecientes) cuendo p se acerca a 0 o a 1. Por lo que vemos en el histograma es obvio que no.  😦  Si alguien sabe como conseguir ese resultado, por el hecho de que pueda tener un error, que me lo haga saber en los comentarios. He intentado jugar con los valores de betaH y betaL pero no hay manera…

Edit: Se ve que el truco está en el valor del parámetro (gracias a un compañero que me lo ha comentado) de , ya que en el modelo, la derivada respecto el trabajo de la función de producción (y despues puesta en por trabajador), la productividad marginal del trabajo es el salario: 

Como se puede ver, los trabajadores reciben una fracción  de la producción final per capita, representa la masa salarial. En las economías como los EE.UU  (y España) se encuentra relativamente estable alrededor de 2/3 de forma que . Ahora, si nos vamos al libro de ‘Economic Growth’ de Barro y XSiM, vemos que comentan que:

Ergo, nos encontramos delante de otro caso de trollscience. Si usamos  u otros valores más altos de  el modelo se comporta como es esperado (salen los resultados que comenta el profesor, que con capital las perturbaciones puntuales en la time preference tienen persistencia):

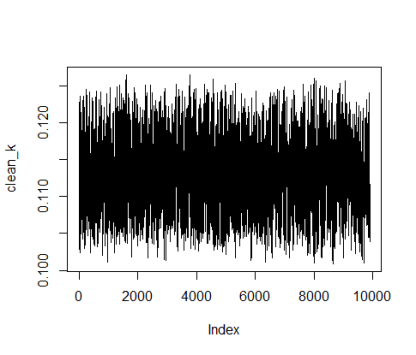
Esto tiene que ver que para alfas muy diferentes de 1, hay significativa desviación de linealidad en la función de producción, lo que causa los resultados iniciales.

pd: si el lector se siente decepcionado por este post simplón lo comprendo, pero irá mejorando en un futuro, y con más R.